Vorlesungsbegleitende Beispielsammlung zur Linearen Algebra I

Diese Sammlung von Applets stellt vorlesungsbegleitende Materialien zur Vorlesung Lineare Algebra I zur Verfügung. Die Materialien umfassen hierbei Themen, die sich nicht nur auf Kernthemen der Linearen Algebra beschränken, sondern auch im weiteren Umfeld der Linearen Algebra interessant sind. Sie umfassen Themen der Gruppentheorie, Symmetrische Gruppen, Komplexe Zahlen, den Fundamentalsatz der Algebra, Kettenbrüche und natürlich viele Aspekte der Linearen Algebra. Die Materialien können als Beispiel in der Vorlesung verwendet werden und auch als Begleitlektüre für Studenten.

Zusatzmaterial: Lineare Algebra Bonbons

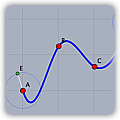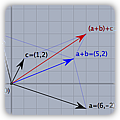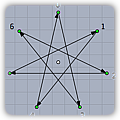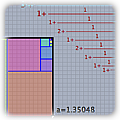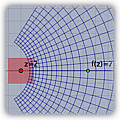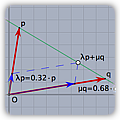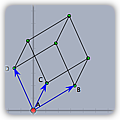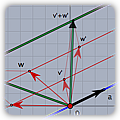1. Einführende Beispiele

Lineare Abbildungen als geometrische Transformationen Gleichgewichte in Spannungsnetzwerken Weichzeichner und Scharfzeichner Glatte Kurven durch Stützstellen Das "Inkreis"-Prädikat

2. Die Gruppenstruktur von $(\mathbb{R}^2,+)$

Addition zweier Elemente Assoziativität

3. Modulorechnen

Gruppentafeln für Addition und Multiplikation Visualisierung der Addition Visualisierung der Multiplikation Vielfache einer Zahl und Sternpolygone Grauwerte der Gruppentafeln

4. Euklidischer Algorithmus und Kettenbrüche

Euklidischer Algorithmus Kettenbruchberechnung Kettenbruchentwicklung einer reellen Zahl (Best-)Aproximierende Brüche

5. Untergruppen von Modulogruppen

Untergruppen von $(\mathbb{Z},+)$ Untergruppen von $(\mathbb{Z}_p,\oplus_p)$ Untergruppen von $(\mathbb{Z}_p,\odot_p)$ für $p = 2,...,17$ Noch mehr Untergruppen von $(\mathbb{Z}_p,\odot_p)$ für $p = 2,...,31$

6. Nebenklassen von Modulogruppen

Nebenklassen von $(\mathbb{Z}_p,\oplus_p)$ Nebenklassen von $(\mathbb{Z}_p,\odot_p)$ Nochmal Nebenklassen von $(\mathbb{Z}_p,\odot_p)$ Die Quotientengruppen von $(\mathbb{Z}_p-\{0\},\odot_p)$ sind zyklisch

7. Die Exponentialfunktion als Gruppenhomomorphismus

Der Rechenschieber Der Body Mass Index (BMI) Calculator

8. Die Symmetrische Gruppe

Die $S_3$ und das Dreieck Das Permutationsknobelspiel (leichte Version) Das Permutationsknobelspiel

9. Komplexe Rechenoperationen

Komplexe Addition Komplexe Multiplikation Komplexe Konjugation Komplexe Potenzen

10. Einheitswurzeln

Die k-ten Wurzeln einer komplexen Zahl $z$ Springende Wurzeln von $z$ Mitverfolgen der Wurzeln von $z$ Experimentieren mit Wurzeln von $z$ $\mathbb{C}$ (für Experten)

11. Taylorreihen

Taylorpolynome von $\sin(x)$ Taylorpolynome von $\cos(x)$ Taylorpolynome von $\exp(x)$ Taylorentwicklung von $\sin(x)$ um einen beliebigen Punkt

12. Komplexe Funktionen I

Welche Terme dominieren bei Polynomen? Welche Terme dominieren bei Polynomen? (Teil II) Bild eines Ursprungkreises unter $f(x) = x^n +x$ Spirographenmuster Spirograph in Wikipedia

13. Komplexe Funktionen II

Komplexe Funktionen (zum Experimentieren) Komplexe Abbildung eines Gitters (für Experten) Bild eines Ursprungskreises Bild eines Ursprungskreises unter einem Polynom Nullstellen eines reellen Polynoms

14. Punkte auf einer Geraden

Darstellung der Punkte auf einer Geraden von p nach q

15. Matrizen, Basen, Lineare Abbildungen

Matrix-Vektor-Multiplikation Projektion eines Würfels Projektion eines Würfels II

16. Quotientenvektorräume

Nebenklassen von Untervektorräumen Addition von Nebenklassen Addition von Nebenklassen II

17. Lineare Abbildungen als geometrische Transformationen

Drehung (Rotation) Drehstreckung Iterierte Drehstreckung Verschiebung (Translation) Affine und projektive Transformationen.

18. Material zu Anwendungen von Determinanten

2x2 Determinante Dreiecksfläche Dreiecksfläche II Fläche eines Polygons Fläche eines Polygons II Berechung der konvexen Hülle Kollisionstest Determinanten in der Geometrie

19. Eigenwerte einer Matrix

Eigenwerte einer Matrix